Morris' Blog

2013-10-08 17:41:25Morris

[高等演算法][作業一] 討論

留言 0 收藏 0 推薦 0

web. The On-Line Encyclopedia of Integer Sequences

1. Recall the recursive program (discussed in the class) that computes the n-th
Fibonacci number. Compute the number of additions used by the program and
design a more efficient program.

2.Determine the space complexity of the quicksort algorithm.

3. Derive a closed formula of T(n) that satisfies the following recurrence relation:
T(n) = T(n/2) + 1, T(1) = 0.

4. Given n >= 1 numbers x1, x2, …, xn, show that the function f(x) = sigma(|x-xi|) takes
its minimum value at the median of these n number.

--> x must be a median of xi.
proof. for sigm(xi-A) has minimum value, A = median(M) of xi

(1) if n is even and A <= M,
x1 <= x2 <= ... <= xs <= A <= xs+1 <= ...<= xt <= M <= xt+1 <= ... <= xn
n = 2t
sigma(xi-A) = sigma{1, s}(A-xi) + sigma{s+1,n}(xi-A)
            = sigma{1, t}(A-M+M-xi)-sigma{s+1, t}(A-xi) + sigma{s+1, t}(xi-A)+sigma{t+1, n}(xi-M+M-A)
            = sigma{1, t}(M-xi)+ t*(A-M) + 2 * sigma{s+1, t}(xi-A) + sigma{t+1, n}(xi-M)+ (n-t)*(M-A)
            = sigma{1, t}(M-xi)+sigma(t+1, n)(xi-M) + 2*sigma{s+1, t}(xi-A) + (n-2t)*(M-A)
            =>         >= 0               >= 0                   ?                 = 0
            when A = M, sigma{s+1, t}(xi-A) has minimum value.
same as A >= M
(2) same as (1)

5. Given a positive integer n, find a way to partition n into one or more positive
integers j1, j2, … , jk (i.e. j1 + j2 + … + jk = n) such that the product of these k
integers is maximized.

f(n) : maximum value of the product of these k integers.

f(2) = 2
f(3) = 3
f(4) = 4 = 2*2
f(5) = 6 = 2*3
f(6) = 9 = 3*3
... (1) f(n) >= n (2) f(n) = max(f(a)*f(b)), for a+b = n, a > 0, b > 0
from (1)&(2), we known that j(i) in {2,3}

let x is numbers of 2, y is numbers of 3
x >= 0, y >= 0.
=> {2x + 3y = n,
   {2^x * 3^y => maximized.
let result = 2^x * 3^y
    log(result) = xlog2 + ylog3
                = xlog2 - (n-2x)/3log3
                = x(log2 - log(3^(2/3))) + n/3 log3
because (log2 - log(3^(2/3))) < 0, get x -> 0

6. Determine the correct closed formula for An (see slide 5 in unit 2 ) and prove its
correctness.

problem: Maximal number of regions obtained by joining n points around a circle by straight lines.

+----------------------------------------------------------------+
PROOF BLOCK. not solved.
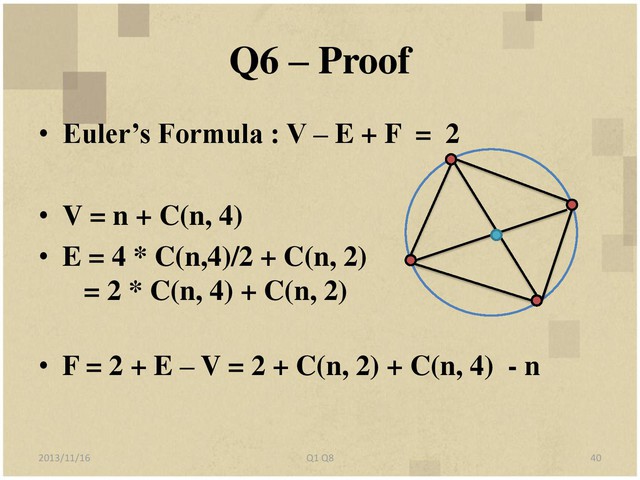
f(n) = 1 + C(n,2) + C(n,4)
T(n + 1) = T(n) + C(n,3) + n
http://www.mathchina.net/dvbbs/dispbbs.asp?boardid=7&Id=4918
http://bbs.csdn.net/topics/300104643
尤拉公式 : V-E+F = 2，點-邊+面 = 2
圓上任三點不共線，將此圖形轉換成平面上的幾個點的連線。
V = n+C(n,4) = 圓上 n 個點 + 圓內弦任四點交於中間那點
E = 4*C(n,4)/2+C(n,2) = 2*C(n,4)+C(n,2)
/*圓內部點相鄰四條邊，由於雙向/2，特別考慮圓內部點與圓上形成的邊只計算一次，補回圓上任兩點構成的邊於其中一弦的一側*/
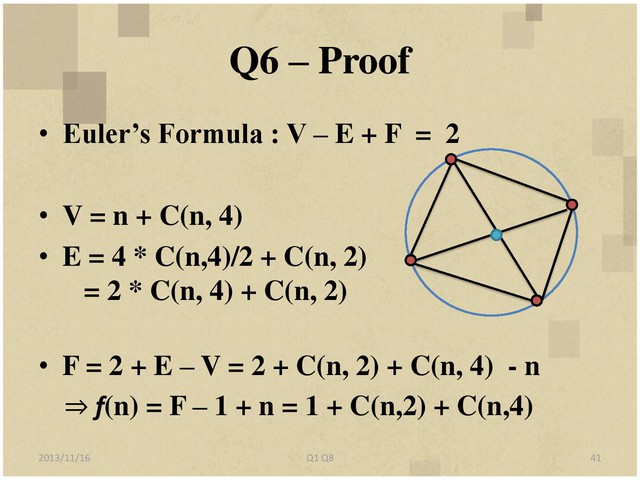
F = 2+E-V = 2+C(n,2)+C(n,4)-n
不考慮最外圍的區域，補回 n 個弓形區域。
=> T(n) = F-1+n = 1+C(n,2)+C(n,4)
+----------------------------------------------------------------+

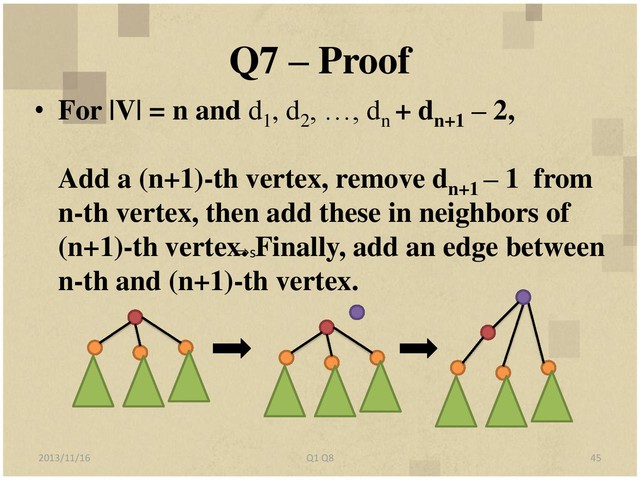
7. Let d1, d2, …, dn, n >= 2, be positive integers. Prove that if d1 + d2 + ... + dn= 2n-2,
then there exists a tree with n vertices of degrees exactly d1, d2, …, dn. Based on
your proof, design an efficient algorithm to construct such a tree.

+----------------------------------------------------------------+
PROOF BLOCK. not solved.
http://math.stackexchange.com/questions/120755/sufficient-conditions-on-degrees-of-vertices-for-existence-of-a-tree
+----------------------------------------------------------------+

build two Queue Q0, Q1
Q0 : if d[i] != 1, i in Q0
Q1 : if d[i] == 1, i in Q1

while(!Q1.empty()) {
    x = Q1.front();
    Q1.pop();
    y = Q0.front();
    Q0.pop();
    show have edge between x and y.
    d[y]--;
    if(d[y] == 1)   Q1.push(y);
    else            Q0.push(y);
}

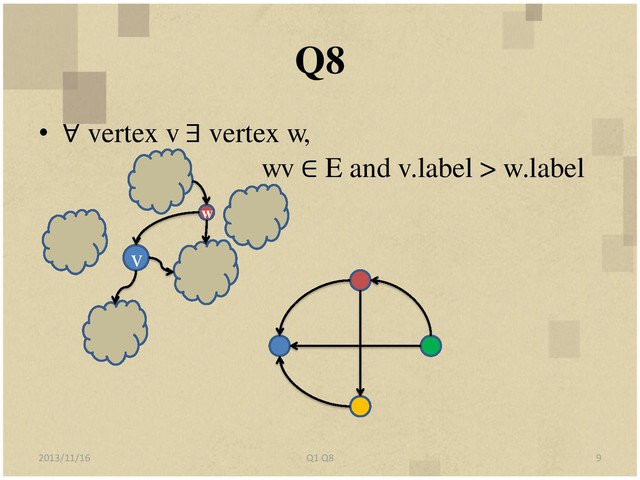
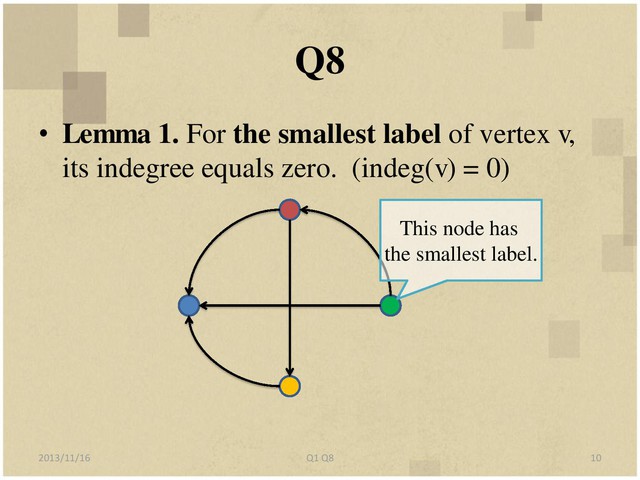
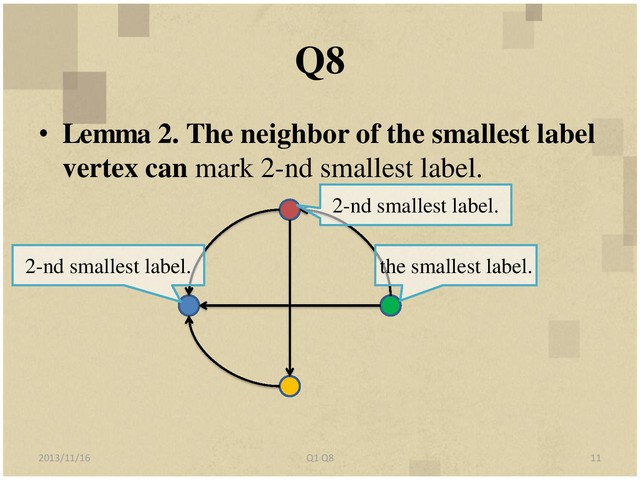
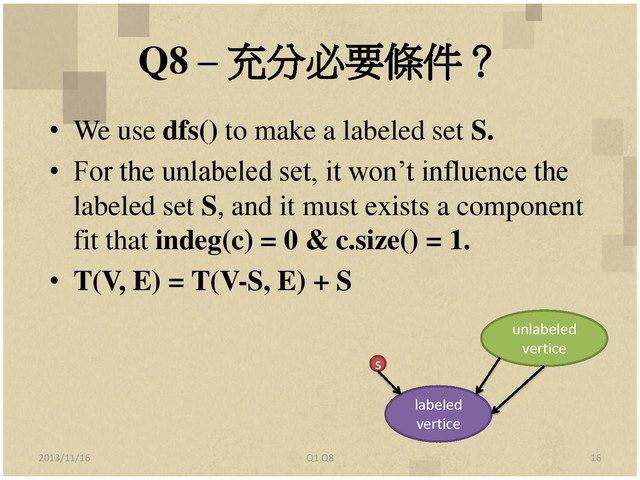
8. Let G=(V, E) be a directed graph (not necessarily acyclic). Design an efficient
algorithm to label the vertices of the graph with distinct labels from 1 to |V| such
that the label of each vertex v is greater than the label of at least one of v’s
predecessors, or determine that no such labeling is possible. (A predecessor of v is
a vertex w such that wv in E.)

待補充分必要條件證明。
+----------------------------------------------------------------+
PROOF BLOCK. not solved.
+----------------------------------------------------------------+

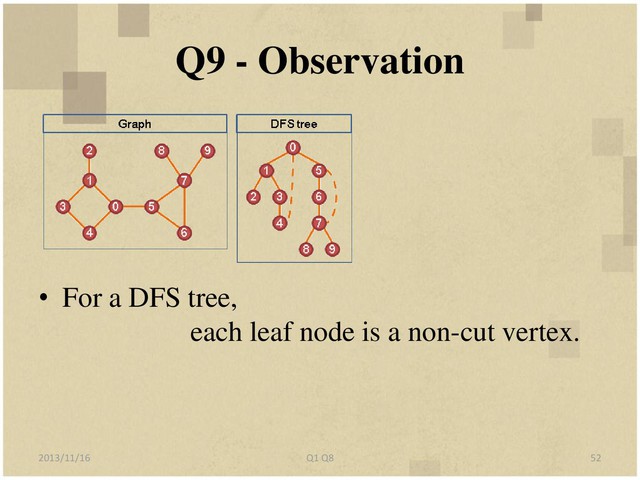
9. For an undirected graph G=(V, E) and a vertex v in V let G-v denote the subgraph
of G obtained by removing v and all the edges incident to v from G. If G is
connected, then G-v can be disconnected or connected. As a matter of fact, for any
connected graph G, we can always find a vertex v in G such that G-v is connected.
Prove this claim by mathematical induction on the numbers of vertices and edges,
respectively. Discuss whether these proving procedures imply algorithms for
finding such a vertex?

Prolem. give an undirected graph G, find one vertex of non-cut vertex.
G & G-v must be a connected graph.

錯誤做法，將會在最下方投影片區更正。

10. Give a linear-time algorithm that takes as input a tree and determines whether it
has a perfect matching: a set of edges that touches each node exactly once.

condition : (a leaf-node) matching (its parent).
            If a leaf-node don't match its parent, tree doesn't have a perfect matching.
            Because it don't have any other node to match.
let T is tree,

step 1. find a leaf-node(u) match its parent (v)
step 2. T' = T-u-v, T' must be a tree.
steo 3. if T' is empty, return true
        else if T' have one node, return false.
        else back step 2.

implement by depth-first search,
mx[] : label of node with matched.
dfs(node, parent) {
    visited[node] = true;
    for i in node's neighbors
        if(visited[i] == false)
            dfs(i, node);
    if(mx[node] == null)
        mx[node] = parent
        mx[parent] = node
}
check all nodes have matched.

12. Let T be an undirected tree. The distance between two vertices in T is the length of
the path connecting these two vertices (neighbors have distance 1). The diameter
of T is the maximal distance over all pairs of vertices. Design an algorithm to find
the diameter of the given tree.

used two dfs() solved.