Morris' Blog

2012-09-22 21:22:39Morris

[ZJ][二分+凸包計算面積] b221. 6. 耕者有其田

留言 1 收藏 0 推薦 0

內容：

在一個遙遠國度的國王有一塊形狀為凸多邊形的田地，長年以來由兩個辛勤的農夫幫忙整地施肥與耕種。這凸多邊形的任兩個頂點所連成的線段一定落於此多邊形之內。由於農夫的努力，此田地的收益帶給了國家許多的財富。為了感謝農夫對王國的貢獻，國王決定將此田地依其面積平均送給這兩個農夫，並把這個任務交由程式設計師來幫忙實現。

程式設計師在此田地的每個頂點依據xy平面實數直角座標系標示了座標。已知所有的頂點都落在x>0的平面上。程式設計師想找出一條通過原點的直線 y=ax (a是一實數係數)，使這直線剛好等分劃過這塊農地。

輸入說明：

輸入檔中所包含之測詴資料的第一行是在測詴資料裡所列出落在該凸多邊形邊上之點(包含頂點)的個數（N ≤100），接下來則是這N個點的座標資料。每一行有兩個整數表示一個點的 x、y 座標 (x、y的絕對值均小於一百萬)，且以一個以上(含一個)的空格分開。在輸入檔中的點座標資料並不一定照順時鐘方向列出。

範例一：

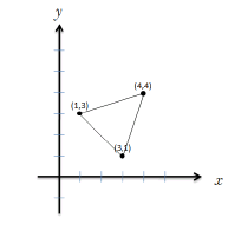
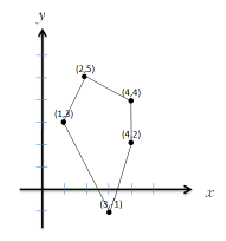
範例二：

輸出說明：

針對所輸入的每組測詴資料，每行輸出對應的實數係數a 的值。精確度到小數點後第四位 (第五位以下四捨五入)。誤差在±0.0001之內都算正確。

範例輸入：

輸入範例 一：
3
1 3
3 1
4 4
輸入範例 二：
5
4 4
4 2
2 5
3 -1
1 3

範例輸出：

輸出範例 一： 
1.0000
輸出範例 二： 
0.9367

提示：

出處：

97全國資訊學科能力競賽

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define eps 1e-6
typedef struct {
    double x, y;
} Pt;
Pt P[500], H[500];
int cmp(const void *i, const void *j) {
    static Pt *a, *b;
    a = (Pt *)i, b = (Pt *)j;
    if(a->x != b->x)
        return a->x < b->x;
    return a->y < b->y;
}
double cross(Pt o, Pt a, Pt b) {
    return (a.x - o.x)*(b.y - o.y) -
            (a.y - o.y)*(b.x - o.x);
}
double calc_area(int n, Pt P[]) {
    static int i;
    double sum = 0;
    for(i = 0; i < n-1; i++)
        sum += P[i].x*P[i+1].y - P[i].y*P[i+1].x;
    return fabs(sum/2);
}
int convex(int n) {
    qsort(P, n, sizeof(Pt), cmp);
    int i, t, m = 0;
    for(i = 0; i < n; i++) {
        while(m >= 2 && cross(H[m-2], H[m-1], P[i]) <= 0)
            m--;
        H[m++] = P[i];
    }
    for(i = n-1, t = m+1; i >= 0; i--) {
        while(m >= t && cross(H[m-2], H[m-1], P[i]) <= 0)
            m--;
        H[m++] = P[i];
    }
    for(i = 0; i < m; i++) P[i] = H[i];
    return m;
}
int main() {
    int n, i;
    while(scanf("%d", &n) == 1) {
        for(i = 0; i < n; i++)
            scanf("%lf %lf", &P[i].x, &P[i].y);
        n = convex(n);
        double A = calc_area(n, P);
        double l = 0xfffffff, r = 0, m;
        double x, y;
        A = A*0.5;
        for(i = 0; i < n; i++) {
            m = P[i].y/P[i].x;
            if(m < l)   l = m;
            if(m > r)   r = m;
        }
        while(fabs(l-r) > eps) {
            m = (l+r)*0.5;
            int it = 0, idx = 0;
            Pt pp[2];
            for(i = 0; i < n-1; i++) {
                if(it == 1)
                    H[idx++] = P[i];
                if((m*P[i].x - P[i].y)*(m*P[i+1].x - P[i+1].y) <= 0) {
                    x = (P[i].x*P[i+1].y - P[i].y*P[i+1].x)/
                        (m*(P[i].x - P[i+1].x) - P[i].y + P[i+1].y);
                    y = m*x;
                    if(it < 2) {
                        if(it == 1) {
                            if(fabs(x-pp[0].x) <= eps && fabs(y-pp[0].y) <= eps)
                                continue;
                        }
                        pp[it].x = x, pp[it].y = y;
                        H[idx++] = pp[it];
                        it++;
                    }
                }
            }
            H[idx++] = pp[0];
            double sum = calc_area(idx, H);
            if(fabs(sum-A) <= eps)
                break;
            if(m*H[1].x-H[1].y <= 0) {
                /*puts("left");*/
                if(sum < A)
                    r = m;
                else
                    l = m;
            } else {
                /*puts("right");*/
                if(sum < A)
                    l = m;
                else
                    r = m;
            }
        }
        printf("%.4lf\n", m);
    }
    return 0;
}

上一篇：[ZJ][數學][代值解] b064. 3. 下界函數

下一篇：[ZJ][N*NlogN][BIT] a533. IOI2004 Day1.1.阿特米斯