[ZJ][數學][代值解] b064. 3. 下界函數
內容 :
很久以前,兩個喜歡研究數字的數學家發現了一種有趣又實用的數列,稱為Davenport-Schinzel 數列。當一個數列滿足以下3 個條件:
1. 數列裡的任何一個數字都會小於或等於一個給定的正整數n
2. 任意兩個相鄰的數字都不會一樣
3. 數列裡找不到兩個數字會間隔地連續出現s+2 次以上(包含s+2 次)
就
稱為 (n, s) Davenport-Schinzel 數列,簡稱 DS(n, s) 數列。例如, (1, 2, 3, 1, 3, 2, 1)
不是一個 DS(3, 3) 數列,當我們從數列中取出 1 和 2 這兩個數字會得到 (1, 2, 1, 2,
1),這兩個數字間隔地連續出現了5 次,所以它違反了第3 個條件。而 (1, 2, 3, 1, 3, 2, 3) 就是一個 DS(3, 3)
數列。
Davenport-Schinzel 數列的性質有許多重要的應用,其中之一就是用來估算一組線性函數 (linear functions) 之下界函數 (lower envelope) 的線段數目。假設 f1, f2, …, fn 是一組線性函數,每一個 fi 都代表一條線段,它們的下界函數 L 的
定義如下:
L(x) = min{fi(x) | 1 ≤ i ≤ n}
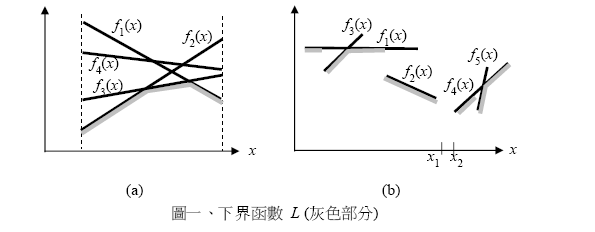
其中 L 的定義域 (domain) 是所有 fi 之定義域的聯集。如果 f1, f2, …, fn 的定義域都相同的話,L 會是一個凸包(convex)形狀的連續函數,如圖一(a);否則 L 可能會是斷斷續續的線段,如圖一(b)。請注意,在圖一(b)中x∈(x1, x2) 並不包含在L 的定義域中。
利用 Davenport-Schinzel 數列來估算下界函式的線段數,需要很複雜的運
算。請你利用電腦程式來幫忙計算一組函數的下界函數包含有多少個線段。在這
個問題裏,你可以假設任兩個 fi 和 fj 不會有重疊或相接成為一條線段的情形,
並且輸入資料中也不會有垂直線的存在。
輸入說明
:
數。
輸出說明
:
輸出 7。
範例輸入 :
4 0 100 100 20 0 20 100 80 0 40 100 50 0 70 100 60 5 0 30 50 30 40 20 70 15 10 20 30 40 80 10 120 40 90 0 110 40
範例輸出 :
3 7
提示
:
出處
:
做法 : 代 x 值, 找不同的連續個數
由於是格子點, 那只好賭一賭, 因為寫線段相交之後又要拆線段有點過於麻煩,
於是決定代值判斷, 因為是格子點, 那麼交點可能會位於不是格子點的部分, +1 可能會有誤差,
因此 x 每次增加 0.5
#include <stdio.h>
typedef struct {
int xr, xl, yr, yl;
} seg;
int main() {
int n, i, j;
seg D[500];
while(scanf("%d", &n) == 1) {
int tmp;
int l = 0xfffff, r = 0;
for(i = 0; i < n; i++) {
scanf("%d %d %d %d", &D[i].xl, &D[i].yl, &D[i].xr, &D[i].yr);
if(D[i].xl > D[i].xr) {
tmp = D[i].xl, D[i].xl = D[i].xr, D[i].xr = tmp;
tmp = D[i].yl, D[i].yl = D[i].yr, D[i].yr = tmp;
}
if(D[i].xl < l) l = D[i].xl;
if(D[i].xr > r) r = D[i].xr;
}
int prev = -1, used;
int ans = 0;
double x;
for(x = l; x <= r; x += 0.5) {
used = -1;
double val = 0xfffff, tmp;
for(j = 0; j < n; j++) {
if(D[j].xl <= x && D[j].xr >= x) {
tmp = D[j].yl - (double)(D[j].yl-D[j].yr)*(D[j].xl-x)/(D[j].xl-D[j].xr);
if(tmp < val) {
val = tmp;
used = j;
}
}
}
if(used == -1) continue;
if(used != prev) {
prev = used;
ans++;
}
}
printf("%d\n", ans);
}
return 0;
}