[ZJ][模擬、旋轉] b125. 積木的拼疊問題(Bricks)
內容 :
小明和同學一起組隊參加拼疊積木比賽,比賽規則如下:
1. 由各隊隊員在限定時間內到運動場的沙地上尋找小積木。
2. 利用找到的小積木,每二個對應為一組,拼成正方形或長方形的大積木。
3. 看看那一隊找到的小積木所組成的大積木面積最大,即可獲勝。
如果我們知道小明這一隊所找到小積木個數與它們的高度和長度,請你寫一個程式算出他們利用這些小積木可以拼出來的大積木的最大面積。
說明:
1. 每個埋在沙中的小積木寬度(W)若為一單位,則長度(L)與高度(H)為一單位的整數倍,且長度與寬度的四個邊中至少有一個邊是整齊的,不會有凹凸的狀況。小積木為實心的,沒有挖洞,而且不會是正方形或長方形,下圖所示為一部份小積木的樣子。
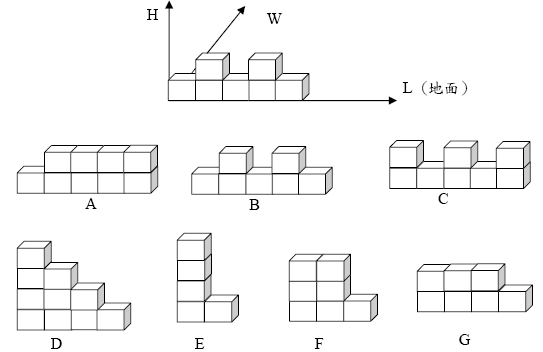
2. 若將小積木整齊的那一個邊對齊坐標軸L,則上圖小積木皆可用一串數字表示,這一串數字的個數等於小積木的長度,而每一個數字則代表其對應的高度。
例
如:小積木A = ( 1, 2, 2, 2, 2)、B = ( 1, 2, 1, 2, 1)、C = ( 2, 1, 2, 1, 2)、D = (
4, 3, 2, 1)、E = ( 4, 1)、F = ( 3, 3, 1)、以及G = ( 2, 2, 2, 1, 1)。
3.
小積木是可以利用旋轉或翻轉來組成正方形或長方形的大積木的,但所組成的大積木必需是實心的,也就是小積木與小積木的接觸面必需密合,中間不能有洞產生。
例如上圖中的小積木B 與C 可以組成一個3×5 的長方形大積木,而E 和 G 則可以組成3×4 的長方形大積木。另外,如果有二個E
就可以組成5×2的長方形大積木,而二個D 可以組成5×4 的正方形大積木了。
條件限制:
1. 小積木的長(L)寬(W)高(H)之範圍如下: W=1、1<L<30、1<H<30。
2. 小積木的個數最多50 個,它們的樣子是可以重覆出現的。
3. 任何一個正方形或長方形的大積木只能由二個小積木組成,但小積木在組合時可以旋轉或翻轉。
4. 若找到的小積木皆無法組成大積木,請輸出0。
輸入說明
:
2. 檔案第二行以後,每一行皆由一串數字組成,數字間利用空白分隔,這一串數字表示一個小積木,表示方式如說明(2)。
輸出說明
:
範例輸入
:
5 1 2 1 2 1 2 1 2 1 2 4 3 2 1 4 3 2 1 1 3 2 1 4 4 1 1 4 1 1 1 2 4 1 2 2 1 1 1 2 1 1 1
範例輸出 :
20 10 10
提示
:
出處
:
旋轉處理限定遞增或遞減情況, 接著就是麻煩的模擬了
#include <cstdio>
#include <sstream>
#include <iostream>
using namespace std;
typedef struct {
int v[100], bt;
} Bricks;
int test(Bricks A, Bricks B) {
int shift, ans = 0, k;
for(shift = 0; shift <= A.bt; shift++) {
int comb[100] = {};
for(k = 0; k < A.bt; k++)
comb[k] = A.v[k];
for(k = 0; k < B.bt; k++)
comb[k+shift] += B.v[k];
int w, h;
w = B.bt+shift > A.bt ? B.bt+shift : A.bt;
h = comb[0];
for(k = 0; k < w; k++)
if(h != comb[k])
break;
if(k == w) {
if(w*h > ans)
ans = w*h;
}
for(k = 0; k < B.bt; k++)
comb[k+shift] += B.v[B.bt-k-1]-B.v[k];
h = comb[0];
for(k = 0; k < w; k++)
if(h != comb[k])
break;
if(k == w) {
if(w*h > ans)
ans = w*h;
}
}
return ans;
}
Bricks rotate(Bricks A) {
Bricks B;
int can = 0, i, j;
for(i = 1; i < A.bt; i++)
if(A.v[i] < A.v[i-1])
break;
if(i == A.bt) can = 1;
for(i = 1; i < A.bt; i++)
if(A.v[i] > A.v[i-1])
break;
if(i == A.bt) can = 2;
if(!can) {
B.bt = -1;
return B;
}
B.bt = A.v[A.bt-1] > A.v[0] ? A.v[A.bt-1] : A.v[0];
for(i = 0; i < B.bt; i++) {
B.v[i] = 0;
for(j = 0; j < A.bt; j++)
if(A.v[j] > i)
B.v[i]++;
}
return B;
}
int main() {
int n;
int i, j, k;
while(scanf("%d", &n) == 1) {
getchar();
string line;
Bricks D[100];
for(i = 0; i < n; i++) {
getline(cin, line);
stringstream sin(line);
D[i].bt = 0;
while(sin>> D[i].v[D[i].bt])
D[i].bt++;
}
int ans = 0;
for(i = 0; i < n; i++) {
for(j = i+1; j < n; j++) {
int tmp = test(D[i], D[j]);
ans = tmp > ans ? tmp : ans;
test(D[j], D[i]);
ans = tmp > ans ? tmp : ans;
Bricks Ra, Rb;
Ra = rotate(D[i]);
Rb = rotate(D[j]);
if(Ra.bt > 0) {
tmp = test(D[j], Ra);
ans = tmp > ans ? tmp : ans;
tmp = test(Ra, D[j]);
ans = tmp > ans ? tmp : ans;
}
if(Rb.bt > 0) {
tmp = test(D[i], Rb);
ans = tmp > ans ? tmp : ans;
tmp = test(Rb, D[i]);
ans = tmp > ans ? tmp : ans;
}
if(Ra.bt > 0 && Rb.bt > 0) {
tmp = test(Ra, Rb);
ans = tmp > ans ? tmp : ans;
tmp = test(Rb, Ra);
ans = tmp > ans ? tmp : ans;
}
}
}
printf("%d\n", ans);
}
return 0;
}
/*
10
1 1 1 3 7
5 7 8 9 2
1 2 3 4 5
1 1 2 2 2 2 3 3 5 6
3 3 4 4 4 4
1 1 1 1 1 1 1 1 1 1 1 1 1 1 2
10 2
2 3 5
10 11 15
1 10 30
*/