[UVA][連通性狀態壓縮] 1501 - Construct the Great Wall
A defensive wall is a fortification used to protect a city or settlement from potential aggressors. From ancient to modern times, they were used to enclose settlements.
Generally, these are referred to as city walls or town walls. Even though, our ancestors decided to build a Great Wall to protect the northern borders of the Chinese Empire against invasion by various nomadic groups.

The map is given as an rectangle area of size N x M. Each grid is an empty area, a city or an enemy. The Great Wall is a simple polygon build alone the edge of the grids, enclosing all the cities and keeping all the enemies out.
The Great Wall is not easy to build, so we should make the Great Wall as short as possible. Now it is your job to calculate the length of the shortest Great Wall so that it can protect all the cities from the enemies.
Input
The first line contains an integer T
(1![]() T
T![]() 50), indicating the
number of test cases.
50), indicating the
number of test cases.
Each test case contains several lines.
The first line contains two integer H, W
(1![]() H, W
H, W![]() 8),
indicating the number of rows and columns of the map.
8),
indicating the number of rows and columns of the map.
The following H lines contains W chars, indicating the map. `o' represents a city, `.' represents a empty area and `x' represents an enemy.
You can assume that there will be at least one city on the map.
Output
For each test case in the input, print one line: `Case #X: Y', where X is the test case number (starting with 1) and Y is the length of the shortest Great Wall (`-1' if impossible).
Hint:
A simple polygon is a closed polygonal chain of line segments in the
plane which do not have points in common other than the common vertices
of pairs of consecutive segments.
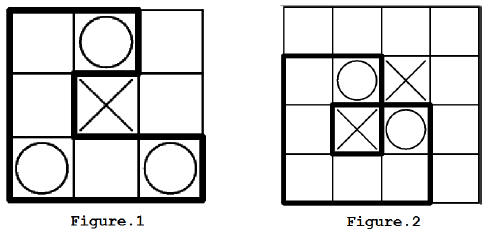
The solution for the first test case in sample is shown in Figure 1.
There is no solution for the second test case because no matter how you build the Great Wall, it will always intersects with itself. (Figure 2).
Sample Input
3 3 3 .o. .x. o.o 4 4 .... .ox. .xo. .... 5 5 .ooo. .x... ..xoo x.xoo .ox.x
Sample Output
Case #1: 14 Case #2: -1 Case #3: 28
[UVa] 1501 - Construct the Great Wall (2011 ACM/ICPC 成都)
題目簡述:
在一個 HxW 的地圖上,用一個連通元件覆蓋所有指定的 'O'。
其中這個連通元件的周長要最小。 // 連通元件必須為簡單多邊形,不可存有內洞,以及邊相交
解題歷程:
由於 H < 9, W < 9,64 bits 恰好一個 long long,
基於搜索狀態期望不會激增的情況下,嘗試了廣搜,但是很不幸的拿
不幸中的萬幸-起碼範例輸入是對的。
最後思考一下動態規劃,這種題目不外乎使用狀態壓縮的插頭動規。
但是為了要考慮要構成一個連通元件,還是自己思考一個動規好了。
於是產生了下列想法 DP[i][j][k]
當前考慮前 i 行,然後在第 i 行上的使用狀況為 j (0/1壓縮)。
而每個分別隸屬於哪個 component // 因為後來會分流合併
ex. 11--2 下一行接上 11111 就是一個合併操作 => 產生 11111
實際估算一下狀態 DP[H][1<<W][?]
由於 ? 處的狀態不能對每一格記錄,如果對每一格記錄會有 maxkind^W。
考慮一行最多 8 個,假使全部相隔最多 4 個元件,這樣 maxkind 也最多是 4。
那麼依序壓縮第 p 個原件是隸屬於哪個 component。
為什麼這麼說呢 ?
ex. 11-2-11 也是有可能的。
曾經建造出
1111111
1-----1
11-2-11
... 最後狀態 DP[8][256][256],轉換作噁。
最後小心內洞
ex. // error transtion
1111--2--11111 // last row status
---1111111---- // now guess ...
很明顯地會發現下方的 1 連接左右的 1 必然存有一個環,這樣就會產生一個洞。
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <queue>
using namespace std;
int dp[10][1<<8][1<<8];
vector<int> getPlace(int O, int X, int W) {
vector<int> ret;
for(int i = (1<<W)-1; i >= 0; i--) {
if((i&O) != O || (i&X) != 0) continue;
ret.push_back(i);
}
return ret;
}
int checkIntersect(int up, int down, int W) {
// xo ox
// ox and xo are Intersect.
for(int i = 1; i < W; i++) {
int LL, LR, RL, RR;
LL = (up>>(i-1))&1;
LR = (up>>(i))&1;
RL = (down>>(i-1))&1;
RR = (down>>(i))&1;
if(LL + LR + RL + RR != 2)
continue;
if(LL == RR || LR == RL)
return 1;
}
return 0;
}
struct DisjointSet {
int parent[20];
void init(int n) {
for(int i = 0; i < n; i++)
parent[i] = i;
}
int findp(int x) {
return parent[x] == x ? x : parent[x] = findp(parent[x]);
}
int joint(int x, int y) {
x = findp(x), y = findp(y);
if(x == y) return 0;
parent[x] = y;
return 1;
}
};
void solve(int H, int W, char g[][10]) {
int last_row = 0;
int rowO[10] = {}, rowX[10] = {};
int i, j, k, p, q, r;
int prev;
for(i = 0; i < H; i++) {
for(j = 0; j < W; j++) {
if(g[i][j] == 'o')
last_row = i;
if(g[i][j] == 'o')
rowO[i] |= 1<<j;
if(g[i][j] == 'x')
rowX[i] |= 1<<j;
}
}
memset(dp, 0x7f, sizeof(dp));
#define oo 0x7f7f7f7f
dp[0][0][0] = 0;
for(i = 0; i < H; i++) {
vector<int> place = getPlace(rowO[i], rowX[i], W);
for(j = 1<<W; j >= 0; j--) {
for(k = 0; k < 256; k++) {
if(dp[i][j][k] == oo)
continue;
int up = j, down;
int upC[4] = {k&3, (k>>2)&3, (k>>4)&3, (k>>6)&3}, upCnt = 0;
int upA[8] = {}, downA[8] = {};
for(p = 0, prev = 0; p < 4; p++) {
int cover = upC[p];
while(prev < W && ((up>>prev)&1) == 0)
prev++;
if(prev < W) upCnt++;
while(prev < W && ((up>>prev)&1) == 1)
upA[prev] = cover, prev++;
}
for(vector<int>::iterator it = place.begin();
it != place.end(); it++) {
down = *it;
if(checkIntersect(up, down, W))
continue;
// build new component assign
int mapped_upC[4] = {-1, -1, -1, -1};
DisjointSet dset; // component[0~3], posY[4~3+W]
dset.init(4+W);
int cnt_upC[4] = {};
for(p = 0, prev = -2; p < W; p++) {
if((down>>p)&1) {
if(prev == p-1)
dset.joint(4+prev, 4+p);
prev = p;
}
}
for(p = 0; p < W; p++) {
if(((down>>p)&1) && ((up>>p)&1)) {
int C = upA[p];
cnt_upC[C]++;
dset.joint(C, 4+p);
}
}
int err = 0;
for(p = 0; p < W; p++) {
if((up>>p)&1) {
int C = upA[p];
if(cnt_upC[C] == 0)
err = 1;
}
}
if(err) continue; // lost one kind of component.
int downKind = 0, downCnt = 0;
int mapped_cc[12];
int downC = 0;
for(p = 0; p < W+4; p++)
mapped_cc[p] = -1;
for(p = 0, prev = -2; p < W; p++) {
if((down>>p)&1) {
if(prev != p-1) {
int parent = dset.findp(p+4);
if(mapped_cc[parent] == -1)
mapped_cc[parent] = downKind++;
downC |= mapped_cc[parent]<<(2*downCnt);
downCnt++;
}
prev = p;
}
}
for(p = 0; p < W; ) { // check don't have a hole.
while(p < W && ((down>>p)&1) == 0)
p++;
if(p >= W) break;
int kind[4] = {};
while(p < W && ((down>>p)&1)) {
if((up>>p)&1) {
kind[upA[p]]++;
if(kind[upA[p]] > 1) {
err = 1;
}
while(p < W && ((down>>p)&1) && ((up>>p)&1))
p++;
} else
p++;
}
}
if(err) {
/*for(p = 0; p < W; p++)
printf("%d", (up>>p)&1);
puts("--- up");
for(p = 0; p < W; p++) {
if(((up>>p)&1) == 0) {
printf("n");
continue;
}
printf("%d", upA[p]);
}
puts("--- upkind");
for(p = 0; p < W; p++)
printf("%d", (down>>p)&1);
puts("--- down");
for(p = 0; p < W; p++) {
if(((down>>p)&1) == 0) {
printf("n");
continue;
}
int parent = dset.findp(p+4);
printf("%d", mapped_cc[parent]);
}
puts("--- downkind");
puts("");*/
continue; // have a hole.
}
if(downKind > 4 || downCnt > 4) {
puts("error !!!");
}
int diff = 0;
for(p = 0; p < W; p++) {
if(((down>>p)&1) == 0)
continue;
int cost = 4;
if(p-1 >= 0 && ((down>>(p-1))&1))
cost -= 2;
if((up>>p)&1)
cost -= 2;
diff += cost;
}
dp[i+1][down][downC] = min(dp[i+1][down][downC], dp[i][up][k] + diff);
}
}
}
}
int ret = oo;
for(i = last_row+1; i <= H; i++) {
for(j = (1<<W)-1; j >= 0; j--)
ret = min(ret, dp[i][j][0]);
}
if(ret == oo) ret = -1;
printf("%d\n", ret);
}
int main() {
// freopen("in.txt", "r+t", stdin);
int testcase, cases = 0;
int H, W;
int i, j, k;
char g[10][10];
scanf("%d", &testcase);
while(testcase--) {
scanf("%d %d", &H, &W);
for(i = 0; i < H; i++)
scanf("%s", g[i]);
printf("Case #%d: ", ++cases);
solve(H, W, g);
}
return 0;
}
/*
10
5 5
.....
..o..
..x..
..o..
.....
3
3 3
.o.
.x.
o.o
4 4
....
.ox.
.xo.
....
5 5
.ooo.
.x...
..xoo
x.xoo
.ox.x
*/