2012-11-08 20:19:57Morris
[ZJ][三年後修訂] d371. 3. Huffman 編碼中的編碼效能問題
內容 :
為了用0 與1 的位元串表示電腦中所需使用的符號,常見的編碼法可分為兩大類:固定長度編碼法與非固定長度編碼法。
固定長度編碼法指的是,將每個符號用相同長度的位元串表示。
例如,要以二進位的0 與1 位元串表示{a, b, c, d, e } 5個符號
每個符號最少需要以3 個位元來編碼成{000, 001, 010, 011, 100}。
但如果我們已知這些符號在多數資料中出現的頻率不同,就可用非固定長度編碼法更有效地表示這些資料
而Huffman 編碼法就是非固定長度編碼法中最常使用的方法。
例如,已知{a, b, c, d, e}這5 個符號的出現頻率由大至小如表一所示。

則Huffman 編碼法利用建立二元樹的方式,首先將每個符號以一個自由節點(freenode)表示
這些自由節點的權重(weight)即是符號的頻率。
接著,從自由節點中找出權重最小的兩個節點,為這兩個節點做一個父節點,此父節點的權重則為這兩個子節點的權重和。
之後,將父節點加入自由節點的行列,並將兩個子節點從自由節點的行列中去除。
接著,重覆選取兩個權重最小的節點,造出父節點並更新自由節點的過程,直到最後只剩一個自由節點為止。
當得到這棵編碼樹後,我們就可以從二元樹的根結點(root node)開始往下走
每往左子樹(left subtree)走一層就給定一個位元的編碼0
每往右子樹(right subtree)走一層就給定一個位元的編碼1
依此方式逐層往下走並同時編碼直到走到葉節點(leaf node)為止。
圖一、二所示即為依表一頻率表所建造的不同Huffman 編碼樹。
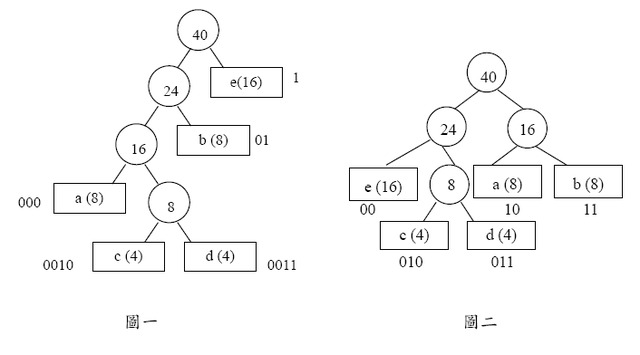
雖然圖一和圖二的編碼結果不同,但檢視其編碼效能,如表二所示,可發現這兩個編碼所得到的總位元數是相同的:
16+24+16+16+16+16=32+16+16+12+12=88。
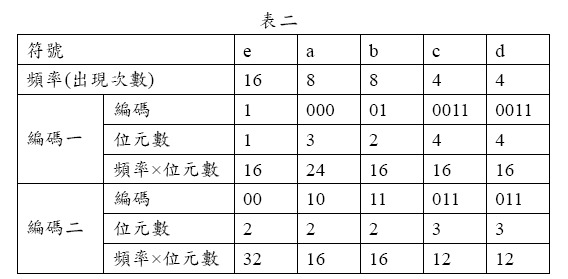
請撰寫一個程式,根據已知的頻率表(尚未排序過),計算以Huffman 編碼後的總位元數。
輸入說明
:
第一行為一個整數n,代表共有幾個符號。(n<=2k,k 為正整數,1<k<=16)。
接下來的n 個數字代表這n 個符號的頻率,每個數字為介於1 與216 之間的正整數,每兩個數字以一個空格隔開。
輸出說明
:
對每一個輸入的頻率表,計算以Huffman 編碼後的總位元數。
範例輸入 :
5 16 8 8 4 4
範例輸出 :
88
提示
:
出處
:
97全國能力縣賽
(管理:pcshic)
/**********************************************************************************/
/* Problem: d371 "3. Huffman 編碼中的編碼效能問題" from 97全國能力縣賽*/
/* Language: CPP (1293 Bytes) */
/* Result: AC(4ms, 771KB) judge by this@ZeroJudge */
/* Author: morris1028 at 2012-11-08 20:14:38 */
/**********************************************************************************/
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
struct ele {
int nd;
long long v;
};
struct NODE {
int l, r;
long long v;
char c;
};
struct cmp {
bool operator() (ele a, ele b) {
return a.v > b.v;
}
};
NODE ND[99999];
long long ans;
void dfs(int nd, int dep) {
if(!ND[nd].l && !ND[nd].r)
ans += dep*ND[nd].v;
if(ND[nd].l)
dfs(ND[nd].l, dep+1);
if(ND[nd].r)
dfs(ND[nd].r, dep+1);
}
int main() {
int n, A[99999];
int i;
while(scanf("%d", &n) == 1) {
priority_queue<ele, vector<ele>, cmp> pQ;
ele l, r, e;
for(i = 1; i <= n; i++) {
scanf("%d", &A[i]);
e.nd = i, e.v = A[i];
ND[i].l = 0, ND[i].r = 0;
ND[i].v = A[i];
pQ.push(e);
}
int size = n;
while(pQ.size() > 1) {
l = pQ.top(), pQ.pop();
r = pQ.top(), pQ.pop();
size++;
e.nd = size, e.v = l.v+r.v;
ND[size].l = l.nd;
ND[size].r = r.nd;
ND[size].v = l.v+r.v;
pQ.push(e);
}
ans = 0;
dfs(size, 0);
printf("%lld\n", ans);
}
return 0;
}
/**********************************************************************************/
/* Problem: d371 "3. Huffman 編碼中的編碼效能問題" from 97全國能力縣賽*/
/* Language: CPP (1293 Bytes) */
/* Result: AC(4ms, 771KB) judge by this@ZeroJudge */
/* Author: morris1028 at 2012-11-08 20:14:38 */
/**********************************************************************************/
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
struct ele {
int nd;
long long v;
};
struct NODE {
int l, r;
long long v;
char c;
};
struct cmp {
bool operator() (ele a, ele b) {
return a.v > b.v;
}
};
NODE ND[99999];
long long ans;
void dfs(int nd, int dep) {
if(!ND[nd].l && !ND[nd].r)
ans += dep*ND[nd].v;
if(ND[nd].l)
dfs(ND[nd].l, dep+1);
if(ND[nd].r)
dfs(ND[nd].r, dep+1);
}
int main() {
int n, A[99999];
int i;
while(scanf("%d", &n) == 1) {
priority_queue<ele, vector<ele>, cmp> pQ;
ele l, r, e;
for(i = 1; i <= n; i++) {
scanf("%d", &A[i]);
e.nd = i, e.v = A[i];
ND[i].l = 0, ND[i].r = 0;
ND[i].v = A[i];
pQ.push(e);
}
int size = n;
while(pQ.size() > 1) {
l = pQ.top(), pQ.pop();
r = pQ.top(), pQ.pop();
size++;
e.nd = size, e.v = l.v+r.v;
ND[size].l = l.nd;
ND[size].r = r.nd;
ND[size].v = l.v+r.v;
pQ.push(e);
}
ans = 0;
dfs(size, 0);
printf("%lld\n", ans);
}
return 0;
}