[ZJ][dp] b220. 5. 蛋糕師傅的煩惱
內容 :
有個蛋糕師傅作蛋糕的方式是先收集每位顧客訂購小蛋糕的大小,然後依照隨機順序將小蛋糕依序組合來決定最後要烘培的蛋糕大小,然後再一刀一刀的切出每個顧客所需的小蛋糕。
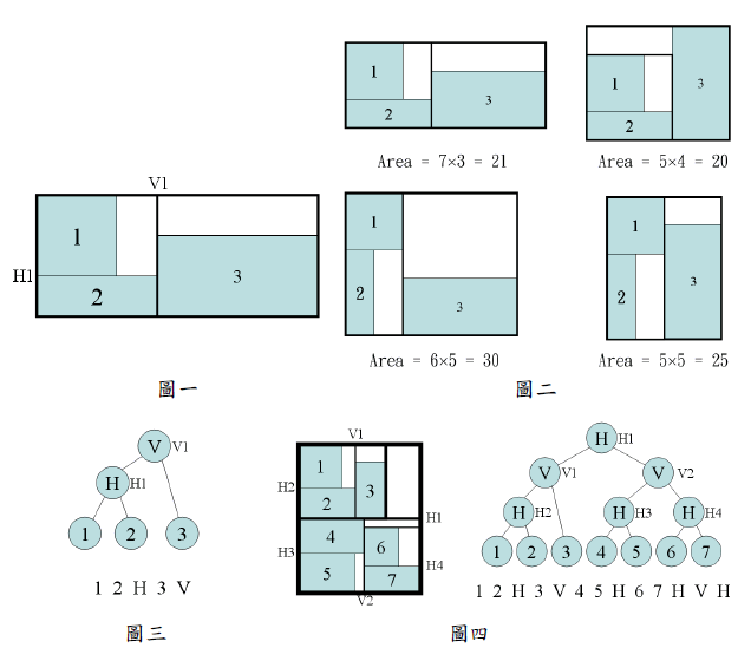
這 裡有兩點要注意的是:(一)、師傅切蛋糕的習慣是每一刀都是以一條直線(水平線或垂直線)將蛋糕一切為二; (二)、是由於前述習慣,所以兩塊小蛋糕所組合出來的形狀一定要是矩形不可以是五邊以上的多邊形。例如有三位顧客訂購蛋糕的大小為1號2*2,2號 3*1,3號4*2,師傅依順序決定 1號排在2號的上面,(1,2,H)表示1號排在2號上面所組成的新矩形,H表示要將1號2號蛋糕分開必須切一刀水平線,(1,2,H)排在3號的左邊, 圖一顯示三塊蛋糕的一種排法,值得注意的是,上下排列時,兩塊小蛋糕的左邊界一定要對齊,左右排列時,兩塊小蛋糕的下邊界一定要對齊,當大蛋糕烘培完成 時,師傅垂直切第一刀後(如圖一V1所示),3號小蛋糕就獨立成型了,再水平切第二刀後(如圖一H1所示),1號和2號蛋糕也分別成型了,最後剩下的就是 把多餘的部份切掉。
在此問題中假設上下或左右的關係已經決定,師傅要煩惱的是蛋糕要不要轉90度擺放,因為不同角度擺放會產生不同的面積,圖二顯示出前述例子因為小蛋糕有否轉90度擺放所產生四種不同面積,其中最小面積為20。
師 傅想到用樹狀圖來計算最小面積的小蛋糕擺法,以圖一為例,此擺法的二元樹狀圖如圖三所示,每個內部節點(internal node)旁邊的符號是相對於圖一裡的切蛋糕切法。針對樹狀圖的節點作後置順序拜訪所得到節點次序如圖三所示。圖四左圖中最外層由最粗線寬所圍繞的矩型為 蛋糕烘培時的面積,經過六刀(例如H1,V1,V2,H2,H3,H4)的切割後,形成7塊各自獨立小蛋糕,切割的流程可用二元樹來表示,圖四右圖下方的 表示式為對此二元樹作後置順序拜訪所得到的節點次序,注意此樹狀圖的中間節點只能是H或V,代表蛋糕切法只能是垂直切或是水平切,而所有的小蛋糕都是落在 樹葉節點(leaf node)。因此本問題的輸入為一後置順序拜訪所得到的樹狀圖節點次序與每個小蛋糕的大小尺寸,你必須在兩秒鐘之內幫蛋糕師傅算出所須最小的烘培蛋糕面 積,所算出的面積不是最小或者是超過十秒鐘才算出答案者都要算失敗沒有通過測詴。
輸入說明
:
輸出說明
:
範例輸入
:
輸入範例1:以圖一為例,其輸入檔案如下: 3 1 2 H V 1 2 2 2 3 1 3 4 2 輸入範例2:以圖二為例,其輸入檔案如下: 1 2 H 3 4 H V 5 6 V H 7 8 H 9 10 H V 11 12 V H V 1 2 5 2 4 3 3 4 2 4 5 3 5 2 4 6 3 1 7 2 6 8 1 4 9 4 2 10 4 5 11 7 8 12 3 5
範例輸出 :
輸出範例1: 輸入範例1的輸出結果如下: 20 輸出範例2: 輸入範例2的輸出結果如下: 221
提示
:
出處
:
其實模擬就可以了,要把樹建出來,對於同一個長記錄一個最小的寬,慢慢合併上去就好。
#include <cstdio>
#include <sstream>
#include <iostream>
#include <algorithm>
#include <map>
using namespace std;
struct node {
int v, op, l, r;
map<int, int> R;
};
stringstream sin;
node nd[1000];
int size;
int w[100], l[100];
void build(int idx) {
string sub;
sin >> sub;
if(sub[0] == 'H') {
nd[idx].l = ++size;
build(size);
nd[idx].r = ++size;
build(size);
nd[idx].op = 1, nd[idx].v = 'H';
} else if(sub[0] == 'V') {
nd[idx].l = ++size;
build(size);
nd[idx].r = ++size;
build(size);
nd[idx].op = 1, nd[idx].v = 'V';
} else {
stringstream nin;
int x;
nin << sub;
nin >> x;
nd[idx].op = 0, nd[idx].v = x;
}
}
void dp(int idx) {
if(nd[idx].op) {
dp(nd[idx].l);
dp(nd[idx].r);
int nl, nw;
for(map<int, int>::iterator it = nd[nd[idx].l].R.begin();
it != nd[nd[idx].l].R.end(); it++) {
for(map<int, int>::iterator jt = nd[nd[idx].r].R.begin();
jt != nd[nd[idx].r].R.end(); jt++) {
if(nd[idx].v == 'H') {
nl = it->first+jt->first;
nw = max(it->second, jt->second);
if(nd[idx].R[nl])
nd[idx].R[nl] = min(nw, nd[idx].R[nl]);
else
nd[idx].R[nl] = nw;
} else {
nl = max(it->first, jt->first);
nw = it->second+jt->second;
if(nd[idx].R[nl])
nd[idx].R[nl] = min(nw, nd[idx].R[nl]);
else
nd[idx].R[nl] = nw;
}
//printf("%d %d %d %d\n", nl, nw, nd[nd[idx].l].v, nd[nd[idx].r].v);
}
}
//puts("");
nd[nd[idx].l].R.clear();
nd[nd[idx].r].R.clear();
} else {
nd[idx].R[l[nd[idx].v]] = w[nd[idx].v];
nd[idx].R[w[nd[idx].v]] = l[nd[idx].v];
}
}
int main() {
string line, stk[1000];
int stkIdx = 0;
getline(cin, line);
stringstream tin;
tin << line;
sin.clear();
while(tin >> line)
stk[stkIdx++] = line;
do {
stkIdx--;
sin << stk[stkIdx] << ' ';
} while(stkIdx > 0);
size = 1;
build(size);
int N, L, W;
while(scanf("%d %d %d", &N, &L, &W) == 3)
l[N] = L, w[N] = W;
dp(1);
int ans = 0xfffffff;
for(map<int, int>::iterator it = nd[1].R.begin();
it != nd[1].R.end(); it++) {
ans = min(ans, it->first * it->second);
}
printf("%d\n", ans);
return 0;
}