[ZJ][插頭DP] a228. 就少一個插座用很不方便
內容 :
小P家裡養了很多隻蛇,他每天都會陪牠們玩。
怎麼玩呢? 他把家裡劃分成N*M的方格,接著把這些蛇擺上地板。
每個方格只能被一隻蛇的身體容納,所以每隻蛇的位置都可以用一串連續方格表示。
這些蛇由於很害羞,所以他們都咬著自己的尾巴。也就是每隻蛇都形成一個環狀。
然而有些格子上有插座,如果一隻蛇佔據了有插座的格子,這樣就少一個插座用很不方便。
所以小P希望有插座的格子不能被蛇佔據。
而且小P也不希望沒有插座的格子上面是空的,也就是希望每個格子都被恰好一隻蛇佔據。
小P給了你他家地板的平面圖,他想問你總共有幾種放蛇的方法能符合上述條件。
因為方法數太多了,請輸出MOD 1000000007的結果
值得注意的是擺幾條蛇完全隨意,你可以一條都不擺或擺二三十條。
輸入說明
:
每筆測資第一行有兩個正整數1 <= N, M <= 11,表示小P家大小。
接下來有N行每行有M個0或1的數字,1表示該格為空、0表示該格有插座。
輸出說明
:
對每筆輸出一行答案,格式如下:
Case(空格)(筆數編號,從1開始):(空格)(答案)
請不要輸出多餘的空白或換行。
範例輸入 :
3 6 3 1 1 1 1 0 1 1 1 1 1 1 1 1 0 1 1 1 1 2 4 1 1 1 1 1 1 1 1 1 1 0
範例輸出 :
Case 1: 3 Case 2: 2 Case 3: 1
提示
:
請相信爆搜不會過。
第一筆範例的解釋:

出處
:

这个状态表示(101111),当前决策格子是第二行第三个格子,显然它已经有了两个插头,也就是有1条线穿过它,所以不用再加插头了。
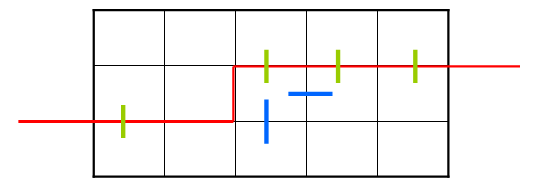

这个状态是(100111)和(101011),当前决策格子是第二行第三个格子,显然有一个插头了,再添加一个即可,那么就有两个选择,要码向下,要码向右,就要有两个转移。
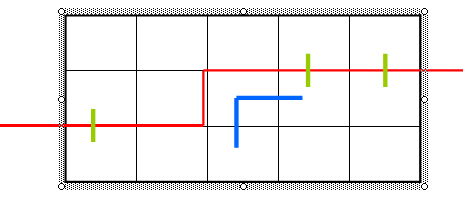
这个状态是(100011),当前决策格子是第二行第三个格子,显然之前没有有一个插头了,只能添加两个,或者不添加,不添加,就肯定不经过这个格子,显然只能这个格子是不可行的。
以上引述 http://blog.csdn.net/xymscau/article/details/67563511.凹角為11:新狀態k'的這兩位均為0,因為兩個度用完了。
2.凹角為01:新狀態k'可以是10或01。
3.凹角為10:新狀態k'可以是10或01。
4.凹角為00:要么11,要么00。 (00的條件是此格為障礙)
#include<stdio.h>
#include<string.h>
main() {
int T, C = 0;
int n, m, k, x;
scanf("%d", &T);
while(T--) {
scanf("%d %d", &n, &m);
long long DP[2][1<<12] ={};
DP[0][0] = 1;
int p, q, i, j, g = 1, h = 0;
int tx, ty;
for(i = 0; i < n; i++) {
for(j = 1; g = 1-g, h = 1-h, j <= m; j++) {
scanf("%d", &x);
for(k = 0; k < 1<<m<<1; k++) {
p = 1 << j, q = p >> 1, tx = (k&p) != 0, ty = (k&q) != 0;
if(x) {
DP[h][k] = DP[g][k^p^q];
if(tx^ty) DP[h][k] += DP[g][k];
} else {
DP[h][k] = tx | ty ? 0 : DP[g][k];
}
}
}
memset(DP[h], 0, sizeof(DP[h]));
for(j = 0; j < (1<<m); j++) DP[h][j<<1] = DP[g][j]%1000000007;
}
printf("Case %d: %d\n", ++C, DP[h][0]);
}
return 0;
}