2012-09-20 22:12:12Morris
[ZJ][一年後修裝版][C++] b113. 6. 線性系統求解
內容 :






輸入說明 :
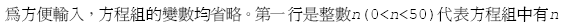

輸出說明 :

本題因為結果為無限組任一輸出不太好確定是否為正確,
所以若結果為無限組的話,輸出N即可。
測資改為多筆測資,
讀完第一個值n後,
後面的方程式請讀到EOF做結束。
(MAPLEWING 2011/01/19修正)
範例輸入 :
[Input 1] <-純粹標明是第幾筆的測資,在測資的輸入裡面並沒有。3 2 8 4 22 5 1 54 10 -1 1[Input 2]31 2 3 08 10 12 67 8 9 6[Input 3]3 1 2 3 04 5 6 37 8 9 0[Input 4]13 10
範例輸出 :
[Output 1] <-純粹標明是第幾筆的測資,您不用輸出這個東西。1x1 = 11x2 = -4x3 = 3[Output 2]N[Output 3]0[Output 4]1x1 = 10/3
提示 :
出處 :
93全國資訊學科能力決賽
#include <cstdio>
#include <iostream>
using namespace std;
class Frac {
public:
long long a, b;
Frac() {
a = 0, b = 1;
}
Frac(int x, int y) {
a = x, b = y;
reduce();
}
Frac operator+(const Frac &y) {
long long ta, tb;
tb = this->b/gcd(this->b, y.b)*y.b;
ta = this->a*(tb/this->b) + y.a*(tb/y.b);
Frac z(ta, tb);
return z;
}
Frac operator-(const Frac &y) {
long long ta, tb;
tb = this->b/gcd(this->b, y.b)*y.b;
ta = this->a*(tb/this->b) - y.a*(tb/y.b);
Frac z(ta, tb);
return z;
}
Frac operator*(const Frac &y) {
long long tx, ty, tz, tw, g;
tx = this->a, ty = y.b;
g = gcd(tx, ty), tx /= g, ty /= g;
tz = this->b, tw = y.a;
g = gcd(tz, tw), tz /= g, tw /= g;
Frac z(tx*tw, ty*tz);
return z;
}
Frac operator/(const Frac &y) {
long long tx, ty, tz, tw, g;
tx = this->a, ty = y.a;
g = gcd(tx, ty), tx /= g, ty /= g;
tz = this->b, tw = y.b;
g = gcd(tz, tw), tz /= g, tw /= g;
Frac z(tx*tw, ty*tz);
return z;
}
private:
static long long gcd(long long x, long long y) {
if(!y) return x;
if(x < 0) x *= -1;
if(y < 0) y *= -1;
long long t;
while(x%y)
t = x, x = y, y = t%y;
return y;
}
void reduce() {
long long g = gcd(a, b);
a /= g, b /= g;
if(b < 0) a *= -1, b *= -1;
}
};
ostream& operator<<(ostream& out, const Frac&x) {
out << x.a;
if(x.b != 1)
out << '/' << x.b;
return out;
}
int main() {
int n, m, i, j, k;
scanf("%d", &n);
m = n;
Frac matrix[m][n+1];
for(i = 0; i < m; i++) {
for(j = 0; j <= n; j++) {
scanf("%lld", &matrix[i][j].a);
}
}
Frac tmp, one(1,1);
int sol = 0;
for(i = 0; i < m; i++) {
int ch = i;
for(j = i; j < m; j++)
if(matrix[j][i].a) {
ch = j;
break;
}
if(i != ch)
for(j = i; j <= n; j++)
tmp = matrix[i][j], matrix[i][j] = matrix[ch][j], matrix[ch][j] = tmp;
if(matrix[i][i].a == 0) {
sol = 1;continue;
}
tmp = one/matrix[i][i];
for(j = i; j <= n; j++)
matrix[i][j] = matrix[i][j]*tmp;
for(j = 0; j < m; j++) {
if(i == j) continue;
tmp = matrix[j][i]/matrix[i][i];
for(k = i; k <= n; k++) {
matrix[j][k] = matrix[j][k] - tmp*matrix[i][k];
}
}
}
if(!sol) {
puts("1");
for(i = 0; i < m; i++) {
printf("x%d = ", i+1);
cout << matrix[i][m] << endl;
}
}
for(i = 0; i < m; i++) {
for(j = 0; j < m; j++) {
if(matrix[i][j].a)
break;
}
if(j == m) {
if(matrix[i][j].a == 0)
sol = 2;
else
sol = 3;
break;
}
}
if(sol == 2)
puts("N");
else if(sol == 3)
puts("0");
return 0;
}
#include <cstdio>
#include <iostream>
using namespace std;
class Frac {
public:
long long a, b;
Frac() {
a = 0, b = 1;
}
Frac(int x, int y) {
a = x, b = y;
reduce();
}
Frac operator+(const Frac &y) {
long long ta, tb;
tb = this->b/gcd(this->b, y.b)*y.b;
ta = this->a*(tb/this->b) + y.a*(tb/y.b);
Frac z(ta, tb);
return z;
}
Frac operator-(const Frac &y) {
long long ta, tb;
tb = this->b/gcd(this->b, y.b)*y.b;
ta = this->a*(tb/this->b) - y.a*(tb/y.b);
Frac z(ta, tb);
return z;
}
Frac operator*(const Frac &y) {
long long tx, ty, tz, tw, g;
tx = this->a, ty = y.b;
g = gcd(tx, ty), tx /= g, ty /= g;
tz = this->b, tw = y.a;
g = gcd(tz, tw), tz /= g, tw /= g;
Frac z(tx*tw, ty*tz);
return z;
}
Frac operator/(const Frac &y) {
long long tx, ty, tz, tw, g;
tx = this->a, ty = y.a;
g = gcd(tx, ty), tx /= g, ty /= g;
tz = this->b, tw = y.b;
g = gcd(tz, tw), tz /= g, tw /= g;
Frac z(tx*tw, ty*tz);
return z;
}
private:
static long long gcd(long long x, long long y) {
if(!y) return x;
if(x < 0) x *= -1;
if(y < 0) y *= -1;
long long t;
while(x%y)
t = x, x = y, y = t%y;
return y;
}
void reduce() {
long long g = gcd(a, b);
a /= g, b /= g;
if(b < 0) a *= -1, b *= -1;
}
};
ostream& operator<<(ostream& out, const Frac&x) {
out << x.a;
if(x.b != 1)
out << '/' << x.b;
return out;
}
int main() {
int n, m, i, j, k;
scanf("%d", &n);
m = n;
Frac matrix[m][n+1];
for(i = 0; i < m; i++) {
for(j = 0; j <= n; j++) {
scanf("%lld", &matrix[i][j].a);
}
}
Frac tmp, one(1,1);
int sol = 0;
for(i = 0; i < m; i++) {
int ch = i;
for(j = i; j < m; j++)
if(matrix[j][i].a) {
ch = j;
break;
}
if(i != ch)
for(j = i; j <= n; j++)
tmp = matrix[i][j], matrix[i][j] = matrix[ch][j], matrix[ch][j] = tmp;
if(matrix[i][i].a == 0) {
sol = 1;continue;
}
tmp = one/matrix[i][i];
for(j = i; j <= n; j++)
matrix[i][j] = matrix[i][j]*tmp;
for(j = 0; j < m; j++) {
if(i == j) continue;
tmp = matrix[j][i]/matrix[i][i];
for(k = i; k <= n; k++) {
matrix[j][k] = matrix[j][k] - tmp*matrix[i][k];
}
}
}
if(!sol) {
puts("1");
for(i = 0; i < m; i++) {
printf("x%d = ", i+1);
cout << matrix[i][m] << endl;
}
}
for(i = 0; i < m; i++) {
for(j = 0; j < m; j++) {
if(matrix[i][j].a)
break;
}
if(j == m) {
if(matrix[i][j].a == 0)
sol = 2;
else
sol = 3;
break;
}
}
if(sol == 2)
puts("N");
else if(sol == 3)
puts("0");
return 0;
}
Frac operator*(const Frac &y) {
若不加 const, 則只能一次操作, 無法進行 a = b+c*d;
兩個以上的運算操作, 跟區域變數的回傳有關, 那是一個屬於系統的物件, 是無法做更改的, 因此要確保不可被修改, 才加上 const 以進行四則運算。
by Inker 指導與心得所感