2012-08-15 16:51:41Morris
[ZJ] d372. 4. 合法執行路徑問題
內容 :
一個程式的執行與程序呼叫(procedure invocation)關係,可以描述成一個流程圖形(flow graph)
例如以下程式,將計算Fibonacci 數值
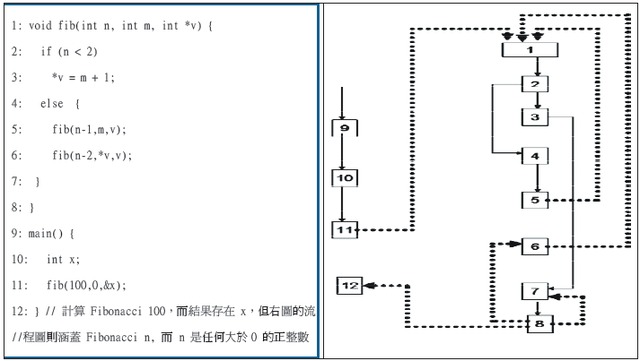
觀察上述程式,每一行指令左邊的數字代表行號(行號為自然數n,若進行函數呼叫時,其返回行號為n+1)
則其流程關係,依照指令的執行先後,可分成程序內部的流程(intra-procedure flow)與跨越程序的流程(inter-procedure flow)。
上述流程圖中,實線表示為程序內部的流程,虛線表示為跨越程序的流程
若遇到程序呼叫(procedure invocation)、與程序結束(procedure return),則產生跨越程序流程
而程序結束時將回到程序呼叫的下一行。考慮之路徑包含所有實線與虛線的流程。
根據上例,行號9 為程式起點,而行號12 為程式結束,以圖形(graph)的路徑(path) 觀點
從端點9 為起點到終點12,可以有不同路徑。
例如路徑9 10 11 1 2 3 7 8 12 為一種走法,我們稱為合法路徑(valid path)
而9 10 11 1 2 4 5 1 2 3 7 8 12 也是一種走法,但因為不合乎程序呼叫的原則
(呼叫程序後,必須返回原呼叫點的下一行)我們稱為不合法路徑(invalid path)。
針對上述程式範例,根據其流程關係所形成之圖形,給予任一由起點到終點的路徑
(只考慮程序進入點與離開點相匹配,也就是呼叫函數後,返回點必須是呼叫點的下一行。不考慮遞迴的次數)
請你寫一個程式來判斷路徑是否為合法。
輸入說明
:
測試檔有許多行,除最後一行外,每行包含一個路徑輸入描述,以序列的行號表示。
行號間以一個或以上的空白隔開,一個路徑描述不會超過100 個數字
例如:
9 10 11 1 2 3 7 8 12
9 10 11 1 2 4 5 1 2 3 7 8 12
最後一行只有包含0 一個整數,代表測試檔案的結束。
輸出說明
:
根據上述範例程式所形成之圖形,依序判斷所給定之路徑是否合法。若合法
輸出:
valid
否則輸出:
invalid
範例輸入 :
9 10 11 1 2 3 7 8 12 9 10 11 1 2 4 5 1 2 3 7 8 12 9 10 11 12 9 10 11 1 2 4 5 1 2 3 7 8 6 1 2 3 7 8 7 8 12 0
範例輸出 :
valid invalid invalid valid
提示
:
出處
:
97全國能力縣賽
(管理:pcshic)
先說這題怎麼解釋, 他問的並不是費氏數列的程序走法, 所以你可能認為判斷會因為 n 有關,
但事實上你看看以下的數據, 你會發現他到一半就是錯的 ?
9 10 11 1 2 4 5 1 2 3 7 8 6 1 2 4 ...
在此題中, 上述的測資是有可能 valid 的, 因此你要忽略跟 n-1, n-2 有關的訊息,
單純按照程序"可能"的走法 ex. 1245(中間一段)6(中間一段)78 或者是 12378 類推
猜題意猜得好辛苦, 為什麼都沒人出來解釋呢 ?
#include <stdio.h>
#include <sstream>
#include <iostream>
using namespace std;
int i;
int dfs(int a[], int n) {
if(a[i] == 1 && a[i+1] == 2 && a[i+2] == 4 && a[i+3] == 5) {
i += 4;
if(dfs(a, n) == 0) return 0;
if(a[i] == 6) {
i++;
if(dfs(a, n) == 0) return 0;
if(a[i] == 7 && a[i+1] == 8) {
i += 2;
return 1;
} else return 0;
} else return 0;
} else if(a[i] == 1 && a[i+1] == 2 && a[i+2] == 3 && a[i+3] == 7 && a[i+4] == 8) {
i += 5;
return 1;
} else return 0;
}
int check(int a[], int n) {
if(a[0] == 9 && a[1] == 10 && a[2] == 11) {
i = 3;
if(dfs(a, n) == 0) return 0;
if(a[i] == 12) return 1;
else return 0;
}
return 0;
}
int main() {
string line;
while(getline(cin, line)) {
stringstream sin;
sin << line;
int a[1000], n = 0;
while(sin >> a[n])
n++;
a[n] = -1;
if(a[0] == 0) break;
printf("%s\n", check(a, n) == 1 ? "valid" : "invalid");
}
return 0;
}
先說這題怎麼解釋, 他問的並不是費氏數列的程序走法, 所以你可能認為判斷會因為 n 有關,
但事實上你看看以下的數據, 你會發現他到一半就是錯的 ?
9 10 11 1 2 4 5 1 2 3 7 8 6 1 2 4 ...
在此題中, 上述的測資是有可能 valid 的, 因此你要忽略跟 n-1, n-2 有關的訊息,
單純按照程序"可能"的走法 ex. 1245(中間一段)6(中間一段)78 或者是 12378 類推
猜題意猜得好辛苦, 為什麼都沒人出來解釋呢 ?
#include <stdio.h>
#include <sstream>
#include <iostream>
using namespace std;
int i;
int dfs(int a[], int n) {
if(a[i] == 1 && a[i+1] == 2 && a[i+2] == 4 && a[i+3] == 5) {
i += 4;
if(dfs(a, n) == 0) return 0;
if(a[i] == 6) {
i++;
if(dfs(a, n) == 0) return 0;
if(a[i] == 7 && a[i+1] == 8) {
i += 2;
return 1;
} else return 0;
} else return 0;
} else if(a[i] == 1 && a[i+1] == 2 && a[i+2] == 3 && a[i+3] == 7 && a[i+4] == 8) {
i += 5;
return 1;
} else return 0;
}
int check(int a[], int n) {
if(a[0] == 9 && a[1] == 10 && a[2] == 11) {
i = 3;
if(dfs(a, n) == 0) return 0;
if(a[i] == 12) return 1;
else return 0;
}
return 0;
}
int main() {
string line;
while(getline(cin, line)) {
stringstream sin;
sin << line;
int a[1000], n = 0;
while(sin >> a[n])
n++;
a[n] = -1;
if(a[0] == 0) break;
printf("%s\n", check(a, n) == 1 ? "valid" : "invalid");
}
return 0;
}