2011-08-24 13:33:32Morris
b113. 6. 線性系統求解
b113. 6. 線性系統求解
作法 : 模擬高斯消元,
特別注意型態的問題, 盡可能約分約掉, 以免溢位,
最後用了 long long 才過
/**********************************************************************************/
/* Problem: b113 "6. 線性系統求解" from 93全國資訊學科能力決賽 */
/* Language: C */
/* Result: AC (0ms, 208KB) on ZeroJudge */
/* Author: morris1028 at 2011-08-24 13:29:55 */
/**********************************************************************************/
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
typedef struct {
long long ele, den;/*ele/den*/
}Fraction;
Fraction Matrix[52][52];
long long GCD(long long x, long long y) {
long long t;
while(x%y) {
t = x, x = y, y = t%y;
}
return y;
}
Fraction F_mod(Fraction A) {/*modify*/
if(A.ele < 0 && A.den < 0)
A.ele *= -1, A.den *= -1;
if(A.ele > 0 && A.den < 0)
A.ele *= -1, A.den *= -1;
return A;
}
Fraction F_divid(Fraction A, Fraction B) {
Fraction C;
C.ele = A.ele * B.den;
C.den = A.den * B.ele;
if(C.ele == 0) {
C.den = 1;
return C;
}
long long t = GCD(fabs(C.ele), fabs(C.den));
C.ele /= t, C.den /= t;
C = F_mod(C);
return C;
}
Fraction F_multi(Fraction A, Fraction B) {
Fraction C;
if(A.ele == 0 || B.ele == 0) {
C.ele = 0, C.den = 1;
return C;
}
long long t = GCD(fabs(A.ele), fabs(B.den));
A.ele /= t, B.den /= t;
t = GCD(fabs(A.den), fabs(B.ele));
A.den /= t, B.ele /= t;
C.ele = A.ele * B.ele;
C.den = A.den * B.den;
C = F_mod(C);
return C;
}
Fraction F_addit(Fraction A, Fraction B) {
long long t = A.den/GCD(A.den, B.den)*B.den;
Fraction C;
C.ele = A.ele*(t/A.den) + B.ele*(t/B.den);
C.den = t;
t = GCD(fabs(C.ele), fabs(C.den));
C.ele /= t, C.den /= t;
C = F_mod(C);
return C;
}
Fraction F_minus(Fraction A, Fraction B) {
long long t = A.den/GCD(A.den, B.den)*B.den;
Fraction C;
C.ele = A.ele*(t/A.den) - B.ele*(t/B.den);
C.den = t;
t = GCD(fabs(C.ele), fabs(C.den));
C.ele /= t, C.den /= t;
C = F_mod(C);
return C;
}
void Print(int n) {
int a, b;
for(a = 0; a < n; a++) {
for(b = 0; b <= n; b++)
printf("(%3lld/%3lld) ", Matrix[a][b].ele, Matrix[a][b].den);
puts("");
}
}
main() {
int n, a, b, c;
scanf("%d", &n);
for(a = 0; a < n; a++) {
for(b = 0; b <= n; b++)
scanf("%lld", &Matrix[a][b].ele), Matrix[a][b].den = 1;
}
int Flag = 0;
for(a = 0; a < n; a++) {
int Idx = -1;
for(b = a; b < n; b++)
if(Matrix[b][a].ele)
{Idx = b;break;}
if(Idx == -1) {continue;}
Fraction tmp;/*Swap*/
for(b = 0; b <= n; b++) {
tmp = Matrix[a][b];
Matrix[a][b] = Matrix[Idx][b];
Matrix[Idx][b] = tmp;
}
Idx = a;
for(b = 0; b < n; b++) {
if(b == Idx) continue;
Fraction X = F_divid(Matrix[b][a], Matrix[Idx][a]);
for(c = 0; c <= n; c++) {
Matrix[b][c] = F_minus(Matrix[b][c], F_multi(Matrix[Idx][c], X));
}
}
}
int time = 0;
for(a = 0; a < n; a++) {
int flag1 = 0;
if(Matrix[a][a].ele)
time++, flag1 = 1;
if(flag1 == 0 && Matrix[a][n].ele)
{Flag = 1;break;}
}
if(time < n && Flag == 0) Flag = 2;
if(Flag == 0) {
Fraction Ans[n];
for(a = n-1; a >= 0; a--) {
Fraction sum;
sum.ele = 0, sum.den = 1;
for(b = a+1; b < n; b++)
sum = F_addit(sum, F_multi(Ans[b], Matrix[a][b]));
sum = F_minus(Matrix[a][n], sum);
Ans[a] = F_divid(sum, Matrix[a][a]);
}
puts("1");
for(a = 0; a < n; a++) {
printf("x%d = ", a+1);
if(Ans[a].den == 1) printf("%lld", Ans[a].ele);
else printf("%lld/%lld", Ans[a].ele, Ans[a].den);
puts("");
}
} else if(Flag == 1) {
puts("0");
} else
puts("N");
return 0;
}
內容 :






輸入說明
:
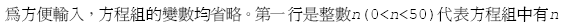

輸出說明
:

本題因為結果為無限組任一輸出不太好確定是否為正確,
所以若結果為無限組的話,輸出N即可。
測資改為多筆測資,
讀完第一個值n後,
後面的方程式請讀到EOF做結束。
(MAPLEWING 2011/01/19修正)
範例輸入 :
[Input 1] <-純粹標明是第幾筆的測資,在測資的輸入裡面並沒有。 3 2 8 4 2 2 5 1 5 4 10 -1 1 [Input 2] 3 1 2 3 0 8 10 12 6 7 8 9 6 [Input 3] 3 1 2 3 0 4 5 6 3 7 8 9 0 [Input 4] 1 3 10
範例輸出 :
[Output 1] <-純粹標明是第幾筆的測資,您不用輸出這個東西。 1 x1 = 11 x2 = -4 x3 = 3 [Output 2] N [Output 3] 0 [Output 4] 1 x1 = 10/3
提示
:
出處
:
93全國資訊學科能力決賽
作法 : 模擬高斯消元,
特別注意型態的問題, 盡可能約分約掉, 以免溢位,
最後用了 long long 才過
/**********************************************************************************/
/* Problem: b113 "6. 線性系統求解" from 93全國資訊學科能力決賽 */
/* Language: C */
/* Result: AC (0ms, 208KB) on ZeroJudge */
/* Author: morris1028 at 2011-08-24 13:29:55 */
/**********************************************************************************/
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
typedef struct {
long long ele, den;/*ele/den*/
}Fraction;
Fraction Matrix[52][52];
long long GCD(long long x, long long y) {
long long t;
while(x%y) {
t = x, x = y, y = t%y;
}
return y;
}
Fraction F_mod(Fraction A) {/*modify*/
if(A.ele < 0 && A.den < 0)
A.ele *= -1, A.den *= -1;
if(A.ele > 0 && A.den < 0)
A.ele *= -1, A.den *= -1;
return A;
}
Fraction F_divid(Fraction A, Fraction B) {
Fraction C;
C.ele = A.ele * B.den;
C.den = A.den * B.ele;
if(C.ele == 0) {
C.den = 1;
return C;
}
long long t = GCD(fabs(C.ele), fabs(C.den));
C.ele /= t, C.den /= t;
C = F_mod(C);
return C;
}
Fraction F_multi(Fraction A, Fraction B) {
Fraction C;
if(A.ele == 0 || B.ele == 0) {
C.ele = 0, C.den = 1;
return C;
}
long long t = GCD(fabs(A.ele), fabs(B.den));
A.ele /= t, B.den /= t;
t = GCD(fabs(A.den), fabs(B.ele));
A.den /= t, B.ele /= t;
C.ele = A.ele * B.ele;
C.den = A.den * B.den;
C = F_mod(C);
return C;
}
Fraction F_addit(Fraction A, Fraction B) {
long long t = A.den/GCD(A.den, B.den)*B.den;
Fraction C;
C.ele = A.ele*(t/A.den) + B.ele*(t/B.den);
C.den = t;
t = GCD(fabs(C.ele), fabs(C.den));
C.ele /= t, C.den /= t;
C = F_mod(C);
return C;
}
Fraction F_minus(Fraction A, Fraction B) {
long long t = A.den/GCD(A.den, B.den)*B.den;
Fraction C;
C.ele = A.ele*(t/A.den) - B.ele*(t/B.den);
C.den = t;
t = GCD(fabs(C.ele), fabs(C.den));
C.ele /= t, C.den /= t;
C = F_mod(C);
return C;
}
void Print(int n) {
int a, b;
for(a = 0; a < n; a++) {
for(b = 0; b <= n; b++)
printf("(%3lld/%3lld) ", Matrix[a][b].ele, Matrix[a][b].den);
puts("");
}
}
main() {
int n, a, b, c;
scanf("%d", &n);
for(a = 0; a < n; a++) {
for(b = 0; b <= n; b++)
scanf("%lld", &Matrix[a][b].ele), Matrix[a][b].den = 1;
}
int Flag = 0;
for(a = 0; a < n; a++) {
int Idx = -1;
for(b = a; b < n; b++)
if(Matrix[b][a].ele)
{Idx = b;break;}
if(Idx == -1) {continue;}
Fraction tmp;/*Swap*/
for(b = 0; b <= n; b++) {
tmp = Matrix[a][b];
Matrix[a][b] = Matrix[Idx][b];
Matrix[Idx][b] = tmp;
}
Idx = a;
for(b = 0; b < n; b++) {
if(b == Idx) continue;
Fraction X = F_divid(Matrix[b][a], Matrix[Idx][a]);
for(c = 0; c <= n; c++) {
Matrix[b][c] = F_minus(Matrix[b][c], F_multi(Matrix[Idx][c], X));
}
}
}
int time = 0;
for(a = 0; a < n; a++) {
int flag1 = 0;
if(Matrix[a][a].ele)
time++, flag1 = 1;
if(flag1 == 0 && Matrix[a][n].ele)
{Flag = 1;break;}
}
if(time < n && Flag == 0) Flag = 2;
if(Flag == 0) {
Fraction Ans[n];
for(a = n-1; a >= 0; a--) {
Fraction sum;
sum.ele = 0, sum.den = 1;
for(b = a+1; b < n; b++)
sum = F_addit(sum, F_multi(Ans[b], Matrix[a][b]));
sum = F_minus(Matrix[a][n], sum);
Ans[a] = F_divid(sum, Matrix[a][a]);
}
puts("1");
for(a = 0; a < n; a++) {
printf("x%d = ", a+1);
if(Ans[a].den == 1) printf("%lld", Ans[a].ele);
else printf("%lld/%lld", Ans[a].ele, Ans[a].den);
puts("");
}
} else if(Flag == 1) {
puts("0");
} else
puts("N");
return 0;
}