2011-07-18 16:11:54Morris
d919. 最大面積
d919. 最大面積
內容
:
給相異的N個格子點
在二維空間中
一條剛好包著所有點的橡皮圈稱為凸包
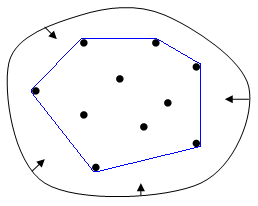
求此凸包的面積(此N個點所能構成的最大面積)
範例圖:

其中圖A為此範例的凸包(面積=7)
而圖B的面積較圖A小,並非為最大面積(面積=6.5)
此時請輸出7
輸入說明
:
每筆測資的第1行為一正整數N(1<=N<=100000)
第2行至第N+1行為正整數Xi,Yi(1<=Xi,Yi<=33000)
輸出說明
:
請輸出此筆測資的凸包面積(這些點所能構成圖形的最大面積)
範例輸入 :
12 2 1 3 1 1 2 2 2 3 2 4 2 1 3 2 3 3 3 4 3 2 4 3 4
範例輸出 :
7
提示
:
出處
:
/**********************************************************************************/
/* Problem: d919 "最大面積" from */
/* Language: C */
/* Result: AC (20ms, 590KB) on ZeroJudge */
/* Author: morris1028 at 2011-07-18 16:07:34 */
/**********************************************************************************/
#include<stdio.h>
typedef struct Point {
int x, y;
}Point;
Point P[100000], CH[100000*2], X[100000];
void MergeSort(int, int);
void Merge(int, int, int);
int cross(Point o, Point a, Point b) {
return (a.x - o.x) * (b.y - o.y) - (a.y - o.y) * (b.x - o.x);
}
void Calc_Area(int m) {
int a, sum = 0;
for(a = 0; a < m-1; a++)
sum += (CH[a].x*CH[a+1].y - CH[a].y*CH[a+1].x);
if(sum&1) printf("%.1lf", sum/2.0);
else printf("%d\n", sum/2);
}
void monotone_chain(int N) {
MergeSort(0, N-1);
int m = 0, a, t;
for(a = 0; a < N; a++) {
while(m >= 2 && cross(CH[m-2], CH[m-1], P[a]) <= 0)
m--;
CH[m++] = P[a];
}
for(a = N-1, t = m+1; a >= 0; a--) {
while(m >= t && cross(CH[m-2], CH[m-1], P[a]) <= 0)
m--;
CH[m++] = P[a];
}
Calc_Area(m);
m--;
return;
}
main() {
int N, a;
while(scanf("%d", &N) == 1) {
for(a = 0; a < N; a++)
scanf("%d %d", &P[a].x, &P[a].y);
monotone_chain(N);
}
return 0;
}
void MergeSort(int l, int h) {
if(l < h) {
int m = (l+h)/2;
MergeSort(l, m);
MergeSort(m+1, h);
Merge(l, m, h);
}
}
void Merge(int l, int m, int h) {
int In1 = l, In2 = m+1;
int a, b, Top = 0;
while(In1 <= m && In2 <= h) {
if(P[In1].x < P[In2].x || (P[In1].x == P[In2].x && P[In1].y < P[In2].y))
X[Top++] = P[In1++];
else
X[Top++] = P[In2++];
}
while(In1 <= m) X[Top++] = P[In1++];
while(In2 <= h) X[Top++] = P[In2++];
for(a = 0, b = l; a < Top; a++, b++)
P[b] = X[a];
}
上一篇:a181. 逆逆向思考