2011-06-21 11:48:59Morris
b058. 3. 關鍵邏輯閘
b058. 3. 關鍵邏輯閘
內容 :
一個組合電路(combinational
circuit)由線路(wires)連接一組邏輯閘(logic gates)而成,並且不包含有向迴路(directed
cycle)。一個組合電路的效能決定於最後一個主要輸出(primary
output)被算出來的時間。假設每一個邏輯閘所需的運算時間都是固定並且是已知的,而線路的延遲(delay)是0。我們希望把一個組合電路所有的關
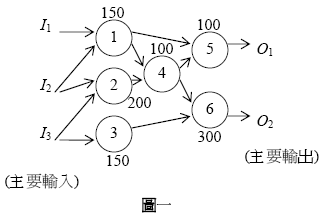
鍵邏輯閘找出來。若一個邏輯閘的運算時間有任何延長,便會影響到整個電路的效能,它就被稱為關鍵邏輯閘。以圖一的組合電路為例,I1、I2、I3是主要輸入;O1、O2是主要輸出;圓圈代表邏輯閘,箭頭代表線路;每個邏輯閘有自己的編號以及固定的延遲時間。在圖一的例子當中,該組合電路中的O1會因為邏輯閘2、4、5的延遲,在時間400才會收到運算結果;而O2會因為邏輯閘2、4、6的延遲,在時間600才收到運算結果,因此O2是最後一個被算出來的主要輸出。關鍵邏輯閘分別是2、4以及6號邏輯閘,當其中一個關鍵邏輯閘的運算時間有任何延長,O2被算出來的時間也會再往後延遲。相反地,就算1號邏輯閘的運算時間從150延長到160,也不會影響到O2被算出來的時間,因此1號邏輯閘並不是關鍵邏輯閘。
輸入說明
:
第一行為一個整數 n (0 < n
< 10000),代表一個組合電路的邏輯閘總數,每個邏輯閘的編號都不同,且範圍是介於 1~n 之間的整數。第二行為一個整數 m (m
< 50000),代表線路的總數。接下來的 n 行,依序列出每個邏輯閘的運算時間;每個運算時間的值是介於 0 到 600
之間(含)的整數。最後 m 行,分別列出每一條線路由某個邏輯閘的輸出接到另一個邏輯閘的輸入。
注意:為簡化輸入,我們把主要輸入(primary inputs)與邏輯閘之間的線路,以及邏輯閘與主要輸出(primary outputs)之間的線路省略。(每一個邏輯閘至少都含有一個線路輸出到另一個邏輯閘或主要輸出)
輸出說明
:
列出關鍵邏輯閘的個數。
範例輸入 :
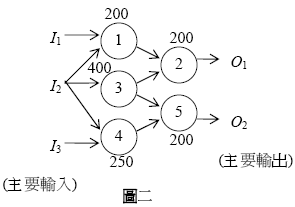
6 6 150 200 150 100 100 300 1 5 1 4 2 4 4 5 4 6 3 6 5 4 200 200 400 250 200 1 2 3 2 3 5 4 5
範例輸出 :
3 3
提示
:
出處
:
95全國資訊學科能力決賽
作法 : DP
題目主要是在講說
由輸入到輸出時間消耗最久的路徑,路徑可能不只有一條,將會出現在最久路徑上的點個數輸出
需要用DP & 回朔找點個數
作法 : DP
題目主要是在講說
由輸入到輸出時間消耗最久的路徑,路徑可能不只有一條,將會出現在最久路徑上的點個數輸出
需要用DP & 回朔找點個數
/**********************************************************************************/
/* Problem: b058 "3. 關鍵邏輯閘" from 95全國資訊學科能力決賽 */
/* Language: C */
/* Result: AC (10ms, 522KB) on ZeroJudge */
/* Author: morris1028 at 2011-06-19 23:12:54 */
/**********************************************************************************/
#include<stdio.h>
typedef struct {
int x, y;
}Link;
Link Next[50001], Pre[50001], X[50001];
int A[10001], DP[10001];
int Sn[10001], Cn[10001], pres[10001], prec[10001];
void MergeSort(int , int, Link[]);
void Merge(int , int , int, Link[]);
int Backtracking(int n) {
int a, b, c, tn, Max = -1;
int Queue[10001], Qt = -1, Used[10001] = {};
for(a = 1; a <= n; a++)
Max = (Max > DP[a]) ? Max : DP[a];
for(a = 1; a <= n; a++)
if(DP[a] == Max)
Queue[++Qt] = a, Used[a] = 1;
for(a = 0; a <= Qt; a++) {
tn = Queue[a];
for(b = 0, c = pres[tn]; b < prec[tn]; b++, c++)
if(DP[tn] == A[tn] + DP[Pre[c].y]) {
if(Used[Pre[c].y] == 0) {
Used[Pre[c].y] = 1;
Queue[++Qt] = Pre[c].y;
}
}
}
return Qt+1;
}
int BFS_DP(int n) {
int a, b, c, tn;
int Queue[20001], Qt = -1, Used[10001] = {};
for(a = 1; a <= n; a++) {
DP[a] = -1;
if(prec[a] == 0)
Queue[++Qt] = a, Used[a] = 1, DP[a] = A[a];
}
for(a = 0; a <= Qt; a++) {
tn = Queue[a];
for(b = 0, c = Sn[tn]; b < Cn[tn]; b++, c++)
if(DP[Next[c].y] < A[Next[c].y] + DP[tn]) {
DP[Next[c].y] = A[Next[c].y] + DP[tn];
if(Used[Next[c].y] == 0) {
Used[Next[c].y] = 1;
Queue[++Qt] = Next[c].y;
}
}
Used[tn] = 0;
}
return Backtracking(n);
}
main() {
int n, m, a, C = 0;
while(scanf("%d %d", &n, &m) == 2) {
for(a = 1; a <= n; a++)
scanf("%d", &A[a]);
for(a = 0; a < m; a++) {
scanf("%d %d", &Next[a].x, &Next[a].y);
Pre[a].x = Next[a].y;
Pre[a].y = Next[a].x;
}
for(a = 1; a <= n; a++)
Sn[a] = -1, Cn[a] = 0, pres[a] = -1, prec[a] = 0;
MergeSort(0, m-1, Next);
MergeSort(0, m-1, Pre);
for(a = 0; a < m; a++) {
if(Sn[Next[a].x] == -1)
Sn[Next[a].x] = a;
Cn[Next[a].x] ++;
}
for(a = 0; a < m; a++) {
if(pres[Pre[a].x] == -1)
pres[Pre[a].x] = a;
prec[Pre[a].x] ++;
}
printf("%d\n", BFS_DP(n));
}
return 0;
}
void Merge(int l, int m, int h, Link Data[]) {
int In1 = l, In2 = m+1;
int a, b, Top = 0;
while(In1 <= m && In2 <= h)
if(Data[In1].x < Data[In2].x)
X[Top++] = Data[In1++];
else X[Top++] = Data[In2++];
while(In1 <= m) X[Top++] = Data[In1++];
while(In2 <= h) X[Top++] = Data[In2++];
for(a = 0, b = l; a < Top; a++, b++)
Data[b] = X[a];
}
void MergeSort(int l, int h, Link Data[]) {
if(l < h) {
int m = (l+h)/2;
MergeSort(l, m, Data);
MergeSort(m+1, h, Data);
Merge(l, m, h, Data);
}
}
上一篇:b060. 5. 快遞服務